Lim căn bậc 3 là một khái niệm rất quan trọng trong giải tích và được sử dụng rộng rãi trong các lĩnh vực khác nhau, từ đại số đến vật lý và kỹ thuật. Bài viết này, Giải mã số học sẽ giải thích khái niệm lim ∛, cách tính và ứng dụng của nó trong toán học.

I. Khái niệm
1.Định nghĩa của lim ∛
Theo định nghĩa, lim căn bậc 3 của một dãy số là giới hạn của các phần tử của dãy đó khi số phần tử tiến đến vô cùng.
Trong toán học, lim ∛ có thể được viết dưới dạng biểu thức toán học như sau:
lim (n → ∞) (a_n)^(1/3)
Trong đó, a_n là một dãy số và (a_n)^(1/3) là căn bậc 3 của a_n.
2.So sánh với lim của hàm số bậc hai và bậc một
Trong khi lim của các hàm số bậc hai và bậc một có thể được tính toán bằng cách sử dụng các phương pháp đơn giản, việc tính toán lim căn bậc 3 thường cần sử dụng các công thức phức tạp hơn.
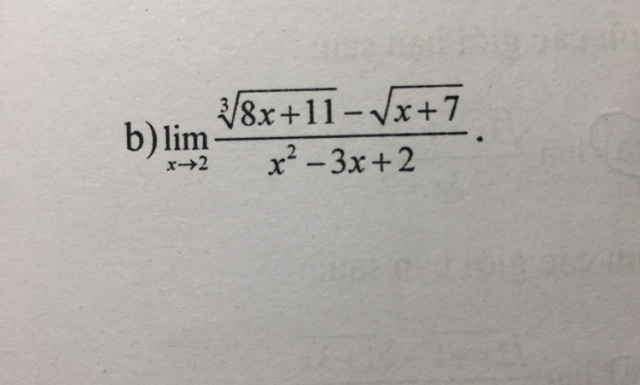
Việc tính toán lim ∛ phức tạp hơn lim của các hàm số khác
II. Cách tính lim ∛
1.Sử dụng công thức L’Hôpital
Điều này cho phép chúng ta tính toán giới hạn của lim căn bậc 3 bằng cách chuyển nó thành một phép tính giới hạn của hàm số.
Cụ thể, công thức L’Hôpital cho phép chúng ta tính toán giới hạn của lim ∛ bằng cách chuyển nó thành giới hạn của hàm số f(x) = (x^3 – a) / (x – b), với a và b là các số cố định.
Sau đó, chúng ta có thể áp dụng công thức L’Hôpital để tính giới hạn của f(x) khi x tiến đến b. Kết quả này sẽ cho chúng ta giá trị của lim ∛.
2.Sử dụng các công thức tính toán khác
Ngoài việc sử dụng công thức L’Hôpital, chúng ta cũng có thể sử dụng các công thức tính toán khác để tính giới hạn của lim ∛.
Các công thức này bao gồm công thức khai triển Taylor và phương pháp giải phương trình đa thức.
III. Ứng dụng của lim căn bậc 3 trong toán học

- Giải quyết các bài toán liên quan đến tập hợp số thực:
Ví dụ: Hãy giải phương trình x^3 – 5x^2 + 8x – 4 = 0. Để tìm nghiệm của phương trình này, ta có thể áp dụng phương pháp dùng lim ∛.
- Ta bắt đầu bằng cách chia đều cả hai vế của phương trình cho x^3: x^3 – 5x^2 + 8x – 4 = 0 ⇒ 1 – 5/x + 8/x^2 – 4/x^3 = 0
- Sau đó, ta sử dụng công thức lim ∛ để tính giới hạn của mỗi thành phần khi x tiến đến vô cùng:
- lim (x -> ∞) 1 = 1
- lim (x -> ∞) (-5/x) = 0
- lim (x -> ∞) (8/x^2) = 0
- lim (x -> ∞) (-4/x^3) = 0
- Vậy giới hạn của phương trình khi x tiến đến vô cùng là 1, tức là phương trình có một nghiệm duy nhất là x = 1.
2. Xác định tính đạo hàm của một hàm số
Lim căn bậc 3 có thể được sử dụng để xác định tính đạo hàm của một hàm số tại một điểm cụ thể. Đây là một trong những ứng dụng quan trọng của lim ∛ trong giải tích.
3. Xác định tính tiệm cận của một hàm số
a. Xác định tính tiệm cận của một hàm số tại vô cùng
Ví dụ: Chúng ta có hàm số f(x) = x^3 – 2x^2 + 5x – 4. Để xác định tính tiệm cận của hàm số này tại vô cùng, ta sử dụng phương pháp dùng lim ∛ như sau:
- Ta chia đều cả hai vế của hàm số cho x^3:
- f(x) = x^3 – 2x^2 + 5x – 4
- ⇒ f(x)/x^3 = 1 – 2/x + 5/x^2 – 4/x^3
- Sau đó, ta tính giới hạn của mỗi thành phần khi x tiến đến vô cùng:
- lim (x -> ∞) 1 = 1
- lim (x -> ∞) (-2/x) = 0
- lim (x -> ∞) (5/x^2) = 0
- lim (x -> ∞) (-4/x^3) = 0
Vậy, giới hạn của hàm số f(x)/x^3 khi x tiến đến vô cùng là 1. Tức là, hàm số f(x) có tính tiệm cận bằng x^3 tại vô cùng.
- Xác định tính tiệm cận của hàm số tại một điểm cụ thể.
Ví dụ, nếu ta muốn xác định tính tiệm cận của hàm số f(x) = x^2 tại x = 2, ta sẽ sử dụng công thức sau:
- lim (x -> 2) (f(x) – f(2))/(x – 2).
Sau đó, ta tính giới hạn của công thức này khi x tiến đến 2 để xác định tính tiệm cận của hàm số tại x = 2.
4. Xác định tính đối xứng của một hàm theo trục đối xứng nào đó.
Ví dụ : ta có hàm số f(x) = x^3 – 3x.
Để xác định tính đối xứng của hàm số này theo trục đối xứng Oy, ta thực hiện thay thế x bằng -x và so sánh kết quả của f(x) và f(-x).
- Nếu f(x) = f(-x) với mọi x, thì hàm số f(x) là đối xứng theo trục đối xứng Oy.
- f(-x) = (-x)^3 – 3(-x) = -x^3 + 3x
- Vậy để xác định tính đối xứng của hàm số f(x) theo trục đối xứng Oy.
- Ta cần giải phương trình f(x) = f(-x), tức là x^3 – 3x = -x^3 + 3x.
- Khi giải phương trình này, ta thu được x = 0.
- Vậy hàm số f(x) là đối xứng theo trục đối xứng Oy, và điểm đối xứng là gốc tọa độ.
IV. Kết luận:
Việc nắm vững khái niệm lim ∛ cũng giúp cho các nhà khoa học và kỹ sư trong các lĩnh vực như vật lý, kỹ thuật và khoa học máy tính có thể áp dụng nó trong nghiên cứu và thiết kế các giải pháp công nghệ.
Lim căn bậc 3 là một khái niệm quan trọng trong toán học và là cơ sở cho nhiều ứng dụng khác nhau. Việc hiểu rõ về cách tính và ứng dụng của nó sẽ giúp cho chúng ta có thể áp dụng nó một cách hiệu quả trong nhiều lĩnh vực khác nhau.
>>> Xem thêm: 15 mét vuông bằng bao nhiêu cm vuông? Hướng dẫn cách đổi





