Đạo hàm được sử dụng rộng rãi trong toán học và các ngành khoa học khác như vật lý, kinh tế học, kỹ thuật và khoa học máy tính để giải quyết các bài toán liên quan đến tốc độ thay đổi và biến động của các hệ thống và quá trình. Trong đó đạo hàm của e mũ u khá phổ biến tại Việt Nam, cùng tìm hiểu các khái niệm và ứng dụng chi tiết trong bài viết sau đây nhé.
Đạo hàm là gì?
Đạo hàm là một khái niệm trong toán học, được sử dụng để tính toán tốc độ thay đổi của một hàm số tại một điểm cụ thể trên đồ thị của nó. Đạo hàm được định nghĩa là giới hạn của tỷ số giữa thay đổi giá trị của hàm số và thay đổi độ dài đoạn trên trục hoành tương ứng khi độ dài đoạn này tiến tới 0. Đạo hàm của một hàm số tại một điểm xác định thường được ký hiệu bằng f'(x) hoặc df(x)/dx.
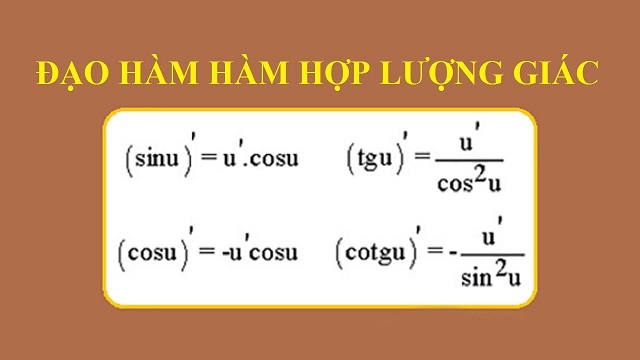
Đạo hàm bao gồm những loại nào?
Trong toán học, có nhiều loại đạo hàm được sử dụng để tính toán tốc độ thay đổi của các hàm số khác nhau. Sau đây là một số loại đạo hàm phổ biến:
-Đạo hàm của hàm số số thực một biến: Đây là loại đạo hàm được sử dụng rộng rãi nhất trong toán học và được định nghĩa bằng giới hạn của tỷ số giữa độ dốc của đường tiếp tuyến tại một điểm trên đồ thị của hàm số và độ dài của đoạn thẳng kết nối điểm đó với một điểm khác trên đường cong.
-Đạo hàm riêng: Đạo hàm riêng là loại đạo hàm của hàm số nhiều biến, được tính bằng cách giữ nguyên một số biến và đạo hàm theo biến còn lại. Đạo hàm riêng được sử dụng rộng rãi trong các ngành khoa học như vật lý, kinh tế học và kỹ thuật.
-Đạo hàm riêng cấp cao: Đây là loại đạo hàm của hàm số nhiều biến, được tính bằng cách lặp lại việc tính đạo hàm riêng nhiều lần cho từng biến. Ví dụ, đạo hàm riêng cấp hai của hàm số f(x, y) được tính bằng cách đạo hàm riêng của đạo hàm riêng theo biến x hoặc y.
-Đạo hàm ngược: Đạo hàm ngược là loại đạo hàm được sử dụng để tìm hàm số ban đầu dựa trên đạo hàm của nó. Đạo hàm ngược thường được sử dụng trong các bài toán tích phân để tìm nguyên hàm của một hàm số đã biết đạo hàm của nó.
Ứng dụng của đạo hàm trong cuộc sống là gì?
Đạo hàm là một khái niệm quan trọng trong toán học và có nhiều ứng dụng trong cuộc sống. Dưới đây là một số ví dụ về ứng dụng của đạo hàm:

-Vật lý: Đạo hàm được sử dụng trong vật lý để tính toán vận tốc, gia tốc và lực. Ví dụ, đạo hàm của vị trí theo thời gian được sử dụng để tính toán vận tốc và đạo hàm của vận tốc theo thời gian được sử dụng để tính toán gia tốc.
-Kinh tế: Đạo hàm được sử dụng trong kinh tế để tính toán độ nhạy của các biến kinh tế đối với các biến khác. Ví dụ, đạo hàm của sản lượng theo vốn đầu tư được sử dụng để tính toán độ nhạy của sản lượng đối với vốn đầu tư.
-Công nghệ: Đạo hàm được sử dụng trong các bài toán liên quan đến tối ưu hóa. Ví dụ, đạo hàm của một hàm mục tiêu được sử dụng để tìm giá trị tối ưu của biến đầu vào.
-Khoa học dữ liệu: Đạo hàm được sử dụng trong học máy để tính toán gradient của hàm mất mát. Gradient được sử dụng để điều chỉnh các tham số trong mô hình để giảm thiểu mất mát.
-Thiết kế và xây dựng: Đạo hàm được sử dụng để tính toán độ dốc của các bề mặt, giúp trong việc thiết kế và xây dựng các kết cấu và sản phẩm.
-Y học: Đạo hàm được sử dụng để tính toán tốc độ thay đổi của các chỉ số sức khỏe, giúp trong việc chẩn đoán và điều trị các bệnh lý.
Đạo hàm của e mũ u là gì?
Đạo hàm của hàm số e^u (trong đó u là một biểu thức phụ thuộc vào một hay nhiều biến số) theo biến số u chính là chính là hàm số e^u:
(d/d u) e^u = e^u
Trong đó, d/d u được hiểu là đạo hàm của hàm số e^u theo biến số u.
Các dạng bài toán của đạo hàm của e mũ u là gì?
Các dạng bài toán của đạo hàm của hàm số e^u (trong đó u là một biểu thức phụ thuộc vào một hay nhiều biến số) có thể liệt kê như sau:
-Tính đạo hàm bậc nhất (hay đạo hàm riêng) của hàm số e^u theo biến số u.
-Tính đạo hàm bậc hai (hay đạo hàm riêng hai) của hàm số e^u theo biến số u.
-Tìm điểm cực trị (điểm tối đa hoặc tối thiểu) của hàm số e^u trên một miền xác định.
-Tìm điểm cực đại và cực tiểu địa phương của hàm số e^u trên một miền xác định.
-Xác định tính chất lồi/lõm của đồ thị của hàm số e^u trên một miền xác định.
-Tìm điểm u mà hàm số e^u đạt cực đại hoặc cực tiểu.
-Tìm giá trị nhỏ nhất hoặc lớn nhất của hàm số e^u trên một miền xác định.
-Xác định đồ thị của hàm số e^u.
Các dạng bài toán này liên quan đến các khái niệm cơ bản của đạo hàm như điểm cực trị, điểm cực đại và cực tiểu, tính chất lồi/lõm của đồ thị hàm số, v.v. Các kỹ năng này rất hữu ích trong việc giải quyết các bài toán ứng dụng của toán học và khoa học tự nhiên. Giải mã số học hy vọng các bạn đã hiểu và ứng dụng của đạo hàm của e mũ u trong cuộc sống.
>>> Xem thêm: Hướng dẫn xét dấu tam thức bậc 3 chi tiết





